

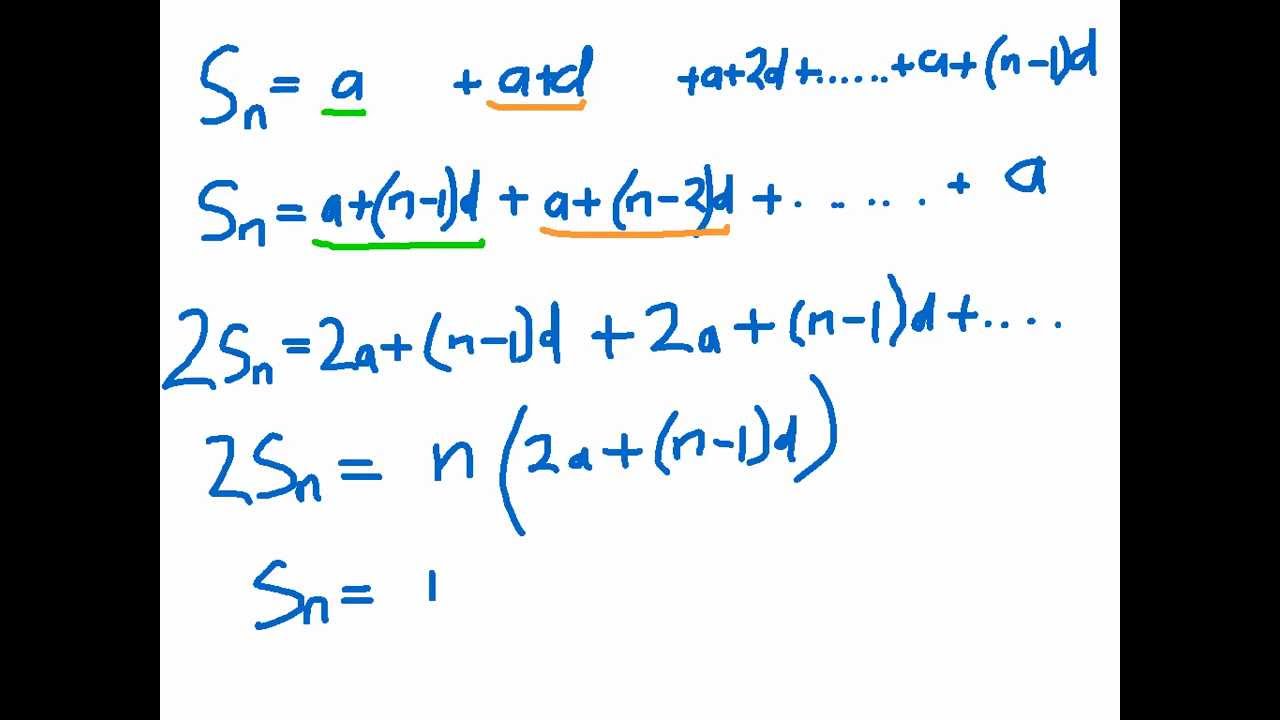
If r r rr is between 1 -1 1minus, 1 and 1 1 11 (i.e. To prove the above theorem and hence develop an understanding the convergence of this infinite series, we will find an expression for the partial sum,, and.
#Sum of geometric sequence proof series
This is, roughly-speaking, why the $r^n$ is missing in the infinite-sum formula. Instead of adding the terms of the sequence by brute force, there is a formula that we can use to easily find the sum of a finite geometric sequence. Say we have an infinite geometric series whose first term is a a aa and common ratio is r r rr. Very quickly, $r^n$ is as close to nothing as makes no difference, and, "at infinity", is ignored. Theorem Let S be a standard number field, that is Q, R or C. The above derivation can be extended to give the formula for infinite series, but requires tools from calculus.įor now, just note that, for $|r|<1$, a basic property of exponential functions is that $r^n$ must get closer and closer to zero as $n$ gets larger. Students should also have completed the following Teaching and Learning Plans: Arithmetic Sequences, Arithmetic Series and Geometric Sequences.


 0 kommentar(er)
0 kommentar(er)
